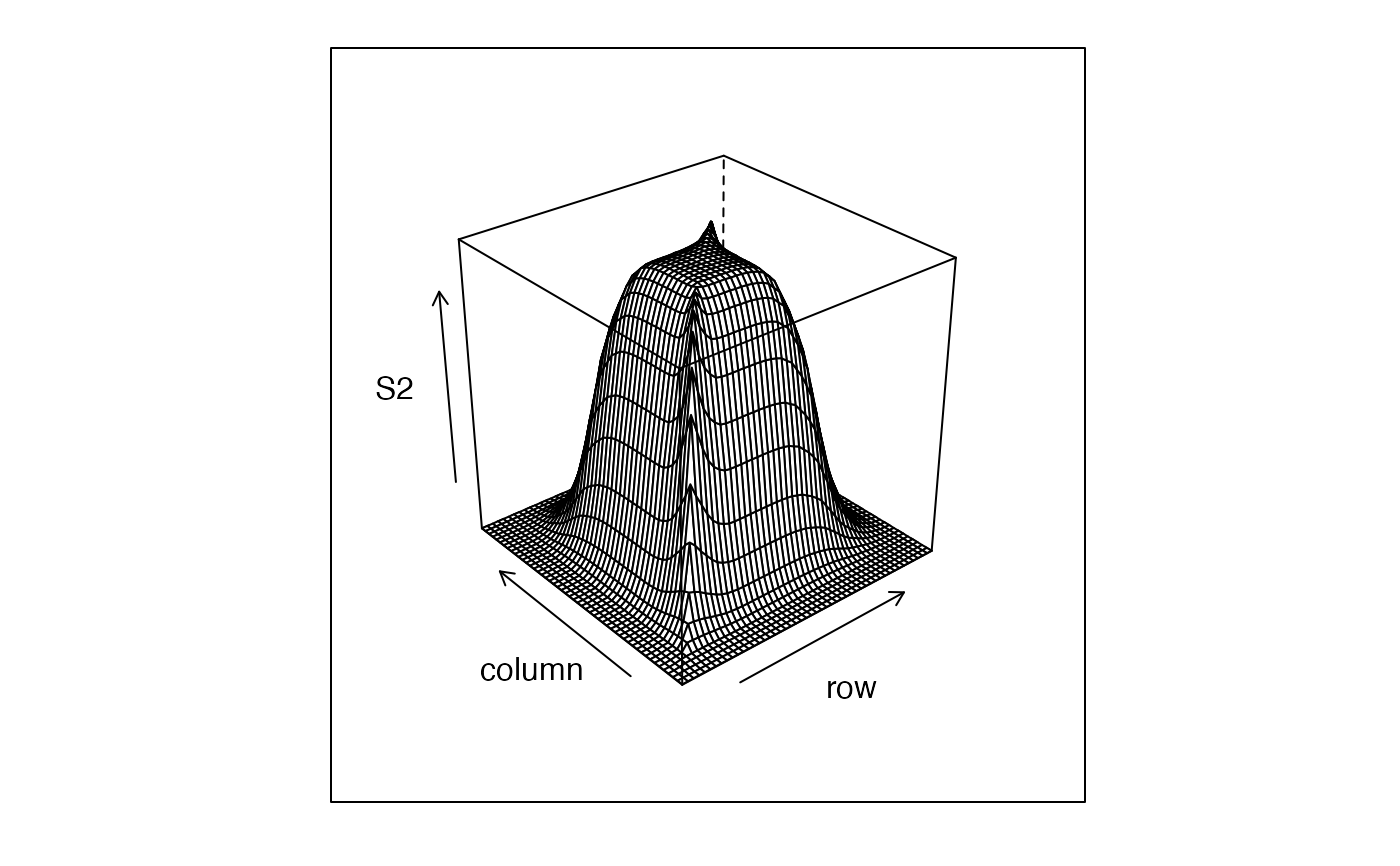
Variance-covariance matrix of the empirical process in an admixture model
Source:R/estimVarCov_empProcess.R
estimVarCov_empProcess.RdEstimate the variance-covariance matrix of some given empirical process, based on the Donsker correlation. Compute Donsker correlation between two time points (x,y) for some given empirical process with R code (another implementation in C++ is also available to speed up this computation).
Arguments
- x
First time point considered for the computation of the correlation given the empirical process.
- y
Second time point considered for the computation of the correlation given the same empirical process.
- obs.data
Sample that permits to estimate the cumulative distribution function (cdf).
- known.p
NULL by default (only useful to compute the exact Donsker correlation). The component weight dedicated to the unknown mixture component if available (in case of simulation studies)
- comp.dist
NULL by default (only useful to compute the exact Donsker correlation). Otherwise, a list with two elements corresponding to component distributions (specified with R native names for these distributions) involved in the admixture model. All elements must be specified, for instance list(f='norm', g='norm').
- comp.param
NULL by default (only useful to compute the exact Donsker correlation). Otherwise, a list with two elements corresponding to the parameters of the component distributions, each element being a list itself. The names used in this list must correspond to the native R argument names for these distributions. All elements must be specified, for instance list(f=NULL, g=list(mean=0,sd=1)).
Author
Xavier Milhaud xavier.milhaud.research@gmail.com
Examples
## Simulate data:
list.comp <- list(f1 = 'norm', g1 = 'norm')
list.param <- list(f1 = list(mean = 12, sd = 0.4),
g1 = list(mean = 16, sd = 0.7))
obs.data <- rsimmix(n=2500, unknownComp_weight=0.5, comp.dist=list.comp, comp.param= list.param)
## Compute the variance-covariance matrix of the corresponding empirical process:
t <- seq(from = min(obs.data$mixt.data), to = max(obs.data$mixt.data), length = 50)
S2 <- sapply(t, function(s1) {
sapply(t, function(s2) {
estimVarCov_empProcess(x = s1, y = s2, obs.data = obs.data$mixt.data) })
})
lattice::wireframe(S2)